It is surprisingly simple to measure jamming (J) to signal (S) ratio, once you get your head around the implications of the J/S equation.  Ends up that a well-constructed test can fix all the RF variables, allowing J/S calculation to be a simple matter of measuring two distances and using your slide rule. 

Jamming to Signal Ratio

Take a close look at the J/S equation in the figure below, especially the deciBel formula.  Despite the fact the receiver and wavelength of operation cancel (kind of amazing on its own), an experiment that holds P_J, G_J, P_T and G_T constant can yield J/S directly.  

By establishing a performance criteria at which the target signal is sufficiently degraded, J/S is calculated by measuring the distances d_j and d_s at which this occurs, then calculating per the formula.  That's it.

Yes, it really is that easy.

Measuring J/S in Practice

By way of example, here's how to do it.  Grab your jammer, round up two friends and give them each a transceiver that works together (or one a transmitter and the other a receiver). Head to a level open field, preferably one that minimizes ground RF reflections at your frequency of operation.  

Set up your jammer, then drop off your friends downrange per the figure here.

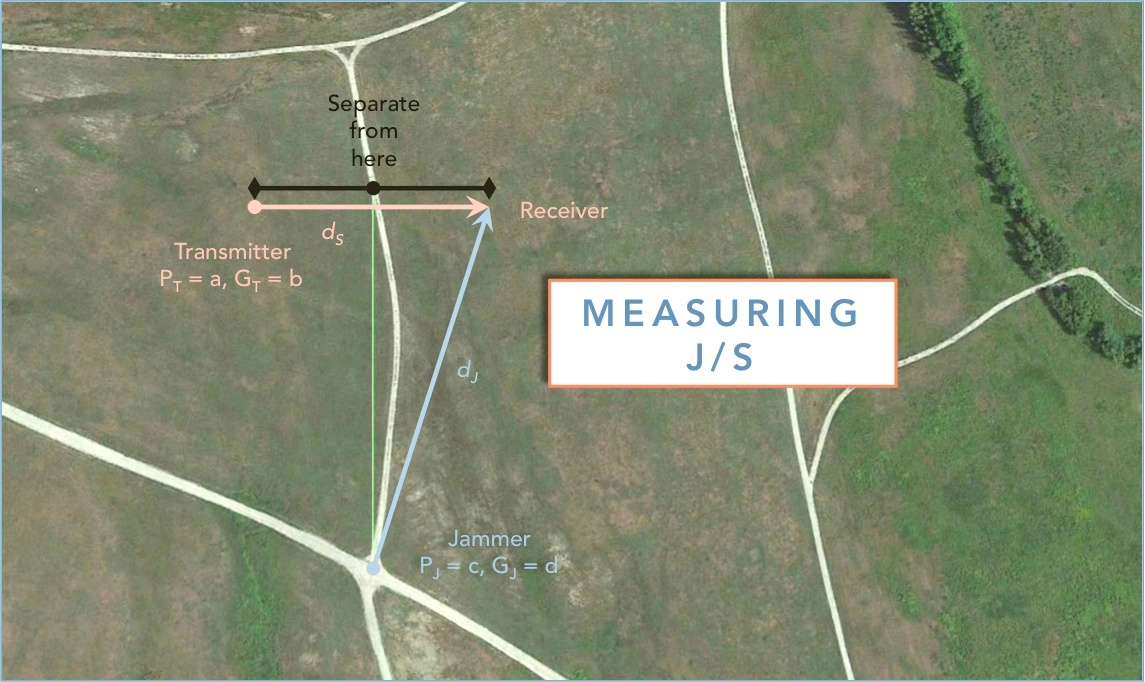Starting next to each other, Friend 1 continuously transmits to Friend 2 as they separate (walking perpendicular to the starting axis to the jammer).  Initially, the friends will have a clear link; F2 will hear F1 with good clarity, in other words, S is much more powerful than J.  

As they separate, d_s increases, while d_j stays about the same, and the signal getting to the receiver becomes more of a mix of the jammer and the transmitter the farther they get apart.

Eventually F2 will not be able to hear F1, hearing only the jammer, at which point they stop walking. J/S at this condition will be close to 1, or 0 dB.  Noting their coordinates or using a range finder, determine the distances d_s and d_j. Then calculate: (in dB)

J/S = P_J + G_J - P_T - G_T + 20*log(d_s) - 20*log(d_j)

Strictly speaking, it doesn't matter what the power level of the jammer and transmitter is, or the gain of each's antenna, as long as they stay constant while testing.   But realistically, it is good to raise the jammer's effective radiated power so that your friends don't have to walk too far.  This may be counter-intuitive.

Say you determine d_s is 40 meters and d_j is 200 m; they differ by -14 dB in the above equation. Therefore, the sum of P_J, G_J, P_T and G_T will be close to 14 dB for our scenario. Note that because of the inverse square law, this test is quite sensitive.  Reducing d_s from 40 to 20 meters increases the transmitter contribution by +6 dB.  

If your jammer can deliver more radiated power at the receiver, a larger signal will be required from the transmitter to overcome it (other parameters held constant). So the only way to raise signal strength S is for your friends to move closer together.  

In most real-world operational scenarios, making your 'frenemies' have to move closer together to communicate by radio is highly desired.  If shouting out loud is more effective than radio, you've won the EW battle and fixed them in time and space!  Check out a previous blog post for a realistic by-the-numbers scenario. 

Want to learn more about how our portfolio of jamming antennas can benefit your system integration? Contact me!